|
|
гУМЦЫуЛњеце§ФЃФтЩњУќЛЙвЊЖрОУ |
| ЗЂВМЪБМфЃК2021-04-05 ЮФеТРДдДЃКЙтУїЭј&жаПЦдКИпФмЫљ фЏРРДЮЪ§ЃК3825 |
 03-31 07:40 03-31 07:40
ЕМгя
ЕБЧАдкМЦЫуПЦбЇЁЂМЦЫуЛњгВМўКЭЩњУќПЦбЇЗНУцЮоЗЈдЄСЯЕФЭЛЦЦПЩФмЛсЪЙЮвУЧГЏзХФПБъТѕНјМЦЫуЛњФЃФтЩњЮябЇЕФЫйЖШИќПьЁЃ

Roland R. NetzЁЂWilliam A. Eaton | зїепедгъЭЄ | выеп
СѕХрдД | ЩѓаЃ
ЕЫвЛбЉ| БрМ

ТлЮФЬтФПЃК
Estimating computational limits on theoretical descriptions of biological cells
ТлЮФЕижЗЃК
https://www.pnas.org/content/118/6/e2022753118
АЃЖћЮТ•бІЖЈкЬдкЫћ1944ФъЕФжјзїЁЖЩњУќЪЧЪВУДЃПЁЗ[1]жаЮЪЕРЃКЁАШчКЮЪЙгУЮяРэМцЛЏбЇЗНЗЈРДНтЪЭдквЛИіЛюЕФгаЛњЬхдкздМКЕФПеМфБпНчФкЗЂЩњЕФЪБПеЪТМўЃПЁБдкЫцКѓЕФНќ80ФъжаЃЌПЦбаШЫдБвбОЬНЫїСЫаэЖргаЙибЧЯИАћЯжЯѓЕФЁЂИќЩюВуЛњРэЕФГЩЙћЁЃЫфШЛШчДЫЃЌвдЕквЛдРэЖдЩњЛюжаЕФЩњУќЬхНјааМЦЫуЛњФЃФтШдШЛЪЧвЛИівЃВЛПЩМАЕФФПБъЁЃ
дкзюНќвЛЦЊЗЂБэгкУРЙњЙњМвПЦбЇдКдКПЏ PNAS ЕФЮФеТжа[2]ЃЌNetz гы Eaton дЄВтСЫетжжФЃФтБфЮЊЯжЪЕЫљашЕФЪБМфЁЃЫћУЧНјвЛВННЋЦфЙРМЦРЉеЙЕНИќДѓЕФЩњЮяЯЕЭГЃЌВЂЬжТлЪЧЗёвдМАКЮЪБгаПЩФмФЃФтжюШчШЫФджЎРрЕФЖрЯИАћЪЕЬхЁЃ
1. гУМЦЫуЛњФЃФтЩњУќЙ§ГЬ
дквЛИіЩњЮябЇЩЯгавтвхЕФЪБМфМфИєФкЃЈР§ШчвЛИіаЁЪБЁЂвЛДЮЯИАћЗжСбЪБМфЃЉЃЌФЃФтЯИАћДѓаЁЕФЗжзгзАХфЫЦКѕЪЧвЛЯюМшОоЕФШЮЮёЁЃЕФШЗЃЌЯжДњЗжзгФЃФтСьгђЕФЪЄРћжЎвЛОЭЪЧЙлВьЕНСЫЕААзжЪЕФПЩФцРЯЛЏЁЊЁЊетжжРЯЛЏЗЂЩњдкЮЂУыМЖ[3]ЁЃЯрБШжЎЯТЃЌЕЅИіЯИАћУПаЁЪБПЩвдКЯГЩЪ§ЧЇЛђЪ§АйЭђИіЕААзжЪЃЌЦфжааэЖрЕААзжЪПЩФмашвЊЪ§УыЛђЪ§ЗжжгВХФмелЕўЃЌВЂЧвжЛгадкЯИАћЛњаЕЃЈcellular machineryЃЉЕФАяжњЯТВХФмЭъГЩЁЃ
дкзюаТЕФПЦбаГЂЪджа[4]ЃЌбаОПепФЃФтСЫЯИАћжЪжаЃЌЯрЖдНЯДѓЕФ100 nmЁС100 nmЁС100 nmбЧПеМфЁЃЕЋЪЧЃЌИУбаОПжаЛёЕУЕФЪ§ЪЎФЩУыЕФЪБМфГпЖШШДЗЧГЃЖЬЃЌБШЫљашЕФ1аЁЪБЖЬСЫ10ИіЪ§СПМЖЃЁЕЋЪЧЃЌШчЙћАДееФІЖћЖЈТЩЕФдЄВтЃЌМЦЫуФмСІМЬајГЪжИЪ§діГЄЃЌФЧУДУжКЯетжжЪБМфГпЖШЩЯЕФВюОрЫЦКѕВЂЗЧвЃВЛПЩМАЁЃ
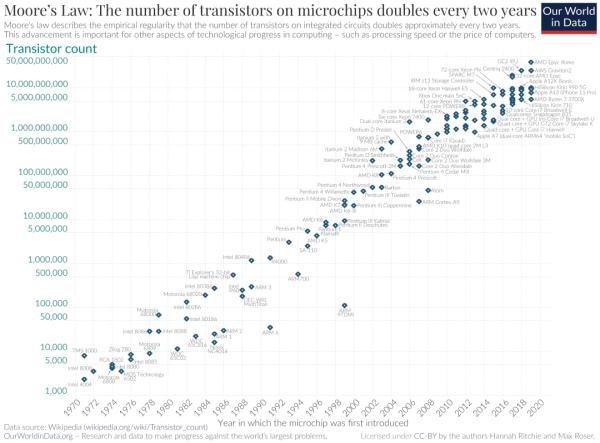
ЭМ1. ФІЖћЖЈТЩШЯЮЊМЏГЩЕчТЗПЩШнФЩЕФОЇЬхЙмЪ§СПЃЌУПИєдМ18ИідТЗБЖЃЌДњБэзХЖдМЦЫуФмСІжИЪ§діГЄЕФЙлВтКЭдЄЦкЁЃЕЋЫцзХаОЦЌзщж№НЅНгНќЕЅИідзгГпЖШЃЌФІЖћЖЈТЩПЩФмЛсЪЇаЇЁЃ
ЕФШЗЃЌШчЙћМЦЫуЛњЫйЖШУП 1.5 ФъЗвЛЗЌЃЌдђгІИУгаПЩФмдк50Фъ[5]ФкДяЕНЫљашЕФЪБМфЗЖЮЇЁЃФГаЉЮЊМгЫйЗжзгФЃФтЖјПЊЗЂЕФЗНЗЈПЩФмЛсЬсЙЉНјвЛВНЕФАяжњЁЃР§ШчЃЌПЩвдГЂЪдЬсИпЗТецЮТЖШвдМгПьЖЏСІбЇЫйЖШЁЃОЁЙметжжМђЕЅЕФМгЫйЖЏСІбЇЕФЗНЗЈДцдкЮЪЬтЁЊЁЊБШШчЮвУЧЮоЗЈЭЈЙ§НЋЦЯЬбОЦдкВЛЦЦЛЕжЪСПЕФЧАЬсЯТЩ§ЮТРДМгЫйРЯЛЏЁЊЁЊЕЋИУЫМТЗШдШЛОпгаЦєЗЂЁЃ
ШЛЖјЃЌДцдквЛИіЙиМќЮЪЬтЃКЗжзгЖЏСІбЇЃЈMolecular dynamicsЃЌMDЃЉзїЮЊБъзМдкдзгМЖЩЯЖдЩњЮяЗжзгЯжЯѓНјааНЈФЃЕФЗНЗЈВЂВЛЪЧеце§ЕФЕквЛЪжЗНЗЈЃКвЊИљОнЕквЛаддРэЗНЗЈЃЈfirst-principles methodЃЉдЄВтЗжзгМфгыЗжзгМфЯрЛЅзїгУЃЌБиаыЮЊЕчзгКЭдзгКЫЧѓНтСПзгбІЖЈкЬЗНГЬЃЈSchrödinger equationЃЉЁЊЁЊеташвЊОоДѓЫуСІЁЃ
2. МђЛЏФЃФтНЕЕЭЫуСІ
ДгЭЗПЊЪМЪЙгУЗжзгЖЏСІбЇЗЈЧѓНтЕФДњМлОЭЪЧПЩЙлЕФМЦЫуГЩБОЁЃЯрБШжЎЯТЃЌБъзМЕФЗжзгЖЏСІбЇЗНЗЈРћгУСЫСНжжМђЛЏЗНЗЈЃК1ЃЉгЩгкЕчзгЕФвЦЖЏЫйЖШБШдзгКЫПьЕУЖрЃЌвђДЫЫќУЧПЩвдЪЙдзгКЫИаЪмЕНгааЇЕФЯрЛЅзїгУЃЛ2ЃЉПЩвдЪЙгУОбщЁАСІГЁЃЈforce fieldЃЉЁБРДНќЫЦетжжгааЇЕФЯрЛЅзїгУЃЌЕЋЫќжЛЪЧУшЪігааЇЪЦФмЫцКЫзјБъЕФКЏЪ§ЖјБфЛЏЕФЗжЮіЙЋЪНЁЃОЙ§Ъ§ЪЎФъЕФХюВЊЗЂеЙЃЌЯждкСІГЁвбЗЧГЃОЋШЗЧвПЩППЁЃВЛавЕФЪЧЃЌЕБЧАЪЙгУЕФДѓЖрЪ§СІГЁШдШЛДцдкЛљБООжЯоадЃКПЦбаШЫдБЮоЗЈЖдЦфНјааЛЏбЇДІРэЁЃ
ЛЏбЇЗДгІЩцМАЙВМлМќКЭЖЯСбКЭаЮГЩЁЃУЛгаЛЏбЇЗДгІЃЌОЭВЛЛсгаЩњУќЁЃЯИАћФкЕФУИДпЛЏаэЖрЛЏбЇЗДгІЃЌАќРЈгыДњаЛЙ§ГЬЛђЛњаЕдЫЖЏВњЩњгаЙиЕФЛЏбЇЗДгІЁЃЮЊСЫУшЪіетжжЗДгІЃЌБиаыНјааСПзгДІРэЁЃNetz КЭ Eaton жИГіЃКавдЫЕФЪЧЃЌВЛашвЊСПзгСІбЇРДУшЪіећИіЕЅдЊЁЃЯрЗДЃЌбаОПШЫдБНіашвЊСПзгСІбЇДІРэРДУшЪіаЮГЩЕФдзгЕФгаЯозгМЏЁЊЁЊШчУИЕФЛюадЮЛЕуМАЦфЕзЮяЁЃ
ЯИАћФЃФтЕФСПзгВПЗжжЕЕУНјвЛВНбаОПЁЃЛЏбЇЗДгІЕФЫйТЪЃЈМДУПЕЅЮЛЪБМфЗЂЩњЗДгІЕФИХТЪЃЉЭЈГЃПЩвдгЩАЂТзФсЮкЫЙЖЈТЩЃЈArrhenius lawЃЉРДУшЪіЃЌ
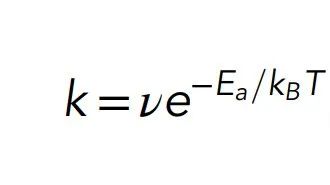
ЦфжаІЭЪЧвЛИіЧАжУвђзгЃЌkBTЪЧШШФмЃЈЕШгкВЃЖћзШТќГЃЪ§КЭЮТЖШЕФГЫЛ§ЃЉЃЌEaЪЧЛюЛЏФмЃЌПЩвдДжТдЕиНтЪЭЮЊуажЕФмСПЁЃдкЗДгІжаЃЌБиаыЬсЙЉИјИУЗжзгЛюЛЏФмEaВХФмЪЙЦфДгЮШЖЈЕФЗжзгЙЙЯѓжаЯћЪЇЃЌДгЖјЙ§ЖЩЕНЗДгІВњЮяЃЈЭМ2ЃЉЁЃШчЙћTЪЧШЫЬхЕФЮТЖШЃЌдђгаkBTЁж0ЃК6kcal = molЁЃ
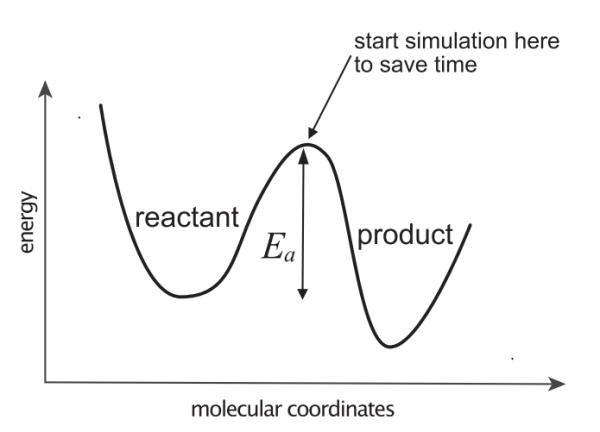
ЭМ2. гУгкМЦЫуЗДгІЫйТЪЕФгааЇФЃФтЗНЗЈЪМгкНЋЯЕЭГжУгкЗДгІЮяКЭВњЮяжЎМфЕФжаМфЮЛжУ
етИіживЊЪ§зжЖдСПзгМЦЫуЫљашЕФОЋЖШЩшжУСЫЯожЦЁЃЕФШЗЃЌИљОнАЂТзФсЮкЫЙЖЈТЩЃЌШєЪЧЙРЫуЛюЛЏФмЪБГіЯж1 kcal / molЕФЮѓВюЃЌдЄВтЕФЗДгІЫйТЪНЋНЕЕЭ5БЖЁЃОЁЙмгавЛаЉСПзгЗНЗЈПЩвдЪЙФмСПМЦЫуЕФОЋЖШдЖаЁгкkBTЃЌЕЋЫуСІашЧѓМЋДѓЃЌЕМжТИУЗНГЬЭЈГЃНіЯогкдкЩйЪ§МИИідзгзщГЩЕФЯЕЭГжаЪЙгУЁЃШЛЖјФПЧАЃЌдкжюШчУИДпЛЏжагіЕНЕФФЧаЉИќИДдгЕФЗжзгЯЕЭГЃЌПЦбаШЫдБвРШЛдкЪЙгУетжжЗНЗЈНјааФЃФтЁЃNetz КЭ Eaton [2] ЬсГіСЫУмЖШЗККЏРэТлЃЈdensity functional theoryЃЌDFTЃЉЗНЗЈ[2]ЁЃDFTЫљашЕФМЦЫуЙЄзїСПгыЯЕЭГЙцФЃЕФСЂЗНГЩе§БШЁЃЕЋЪЧDFTЕФЕБЧАОЋЖШЭЈГЃНіЮЊМИЧЇПЈУПФІЖћ[6]ЃЌвђДЫЃЌЭЈЙ§ЛљгкDFTЕФФЃФтЫљдЄВтЕФЖЏЬЌЪБМфГпЖШНЋЬсЩ§вЛИіЪ§СПМЖЁЃгШЦфашвЊзЂвтЕФЪЧЃЌгыЦфЫћЕчзгНсЙЙЗНЗЈВЛЭЌЃЌDFTВЂУЛгаЬсЙЉЯЕЭГЕФЗНЗЈЃЌЭЈЙ§аоИФИќИФМЦЫуВЮЪ§вдЬсИпЦфзМШЗадЁЃ
ЙРМЦЪБМфГпЖШЩЯЕФЪ§СПМЖЮѓВюБОЩэВЂВЛЪЧжТУќЕФЃКШчЙћЗТецжаЗЂЩњЕФЫљгаЙ§ГЬЖМБШЪЕМЪЫйЖШПьЪЎБЖЃЌдђМђЕЅЕФж№ВНЩ§МЖНЋЛжИДе§ШЗЕФЖЏСІбЇЁЃЕЋЪЧЃЌЯыЯѓвЛЯТФГаЉЙ§ГЬЗЂЩњЕФЫйЖШПьСЫЪЎБЖЃЌЖјЦфЫћЙ§ГЬЗЂЩњЕФЫйЖШШДТ§СЫЪЎБЖЃКетНЋбЯжиЦЦЛЕВЛЭЌЙ§ГЬЕФЯрЖдЫйТЪЁЃвђДЫЃЌдкЗТецжаВЛЛсБЃСєЪЪЕБЯИАћЙІФмЫљашЕФЯрЖдЫйТЪЕФОЋУюЦНКтЃЌЕМжТЦфдЄВтФмСІЕФЯТНЕЁЃ
етаЉПМТЧвђЫиБэУїЃЌГ§ЗЧDFTЕФзМШЗадЕУЕНЯдзХЬсИпЃЈзюНќЛљгкЛњЦїбЇЯАЕФDFTЗНЗЈдкетЗНУцЫЦКѕКмгаЯЃЭћ[6]ЃЉЃЌЗёдђВЂВЛЪЕгУЁЃШЛЖјЃЌПЩФмашвЊЛЈЗбДѓСПГЩБОЕФСПзгМЦЫуВХФмЛёЕУЫљашЕФдЄВтФмСІЁЃгЩгкМЦЫуГЩБОгыЫљашОЋЖШжЎМфДцдкЗДБШЙиЯЕЃЌвђДЫПЩвдНЋетжжЙиЯЕЪгЮЊ Netz КЭ Eaton ЬсГіЕФЁАЩњЮяВЛШЗЖЈадЙиЯЕЃЈbiological uncertainty relationshipsЃЉЁБжЎвЛЁЃ
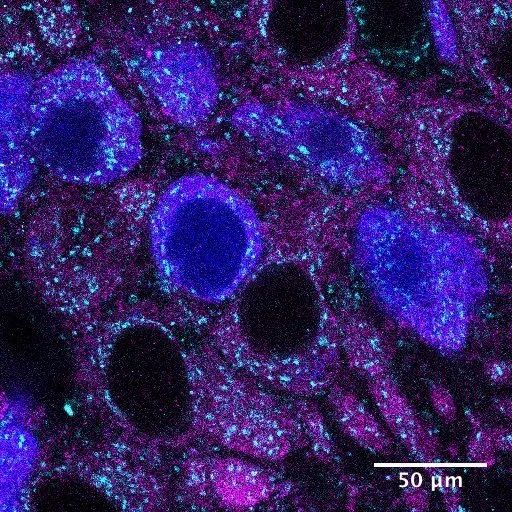
ЭМ3. бЧЯИАћНсЙЙЙлВтМАЦфЮяРэЛњжЦЭЦВтвбгаНЯЖрбаОПЃЌЕЋДПМЦЫуЛњФЃФтШдШЛРЇФбЁЃЭМЮЊвдКЃТэЧјЩёОдЊЯИАћЕФбЧЯИАћНсЙЙ
ЮвУЧвбОСЫНтСЫКмЖргаЙибЧЯИАћЯжЯѓЕФЮяРэЛњжЦЃЌЕЋЪЧЪЙгУЕквЛдРэЖдЛюЖЏжаЕФЛюЯИАћНјааМЦЫуЛњФЃФтШдШЛЪЧвЛИівЃВЛПЩМАЕФФПБъЁЃЛљгкзюНќ Netz КЭ Eaton дкетЦЊЮФеТжаИјГіЕФдЄВтЃЌдкетбљЕФФЃФтБфЮЊЯжЪЕжЎЧАЃЌЮвУЧНЋашвЊЕШД§ЖрГЄЪБМфЁЃ
ОЁЙмвЛИідзгМЖЕФгАЦЌТ§ЫйВЅЗХжСвЛИіаЁЪБЛсСюШЫаЫЗмЃЌЕЋгЩгкСэвЛИідвђЃЌЫќПЩФмУЛгаЬЋДѓЕФдЄВтФмСІЃКДѓЖрЪ§ЯИАћЯжЯѓЖМдкдЫааЃЌШЛЖјЯжгаЪжЖЮжЛФмЭЈЙ§ЖрДЮжиИДФЃФтРДЛ§РлзуЙЛЕФЭГМЦаХЯЂКѓВХФмРэНтЁЃдкетЗНУцЃЌЯжДњЕФЁАЯИАћбЇЃЈcellingЃЉЁБЗНЗЈНтОіГЄЦкЖЏСІбЇЮЪЬтЫЦКѕЬиБ№гаЯЃЭћГЩЮЊвЛжжВЙОШДыЪЉЁЃетЬздзгТлЗНЗЈНЋЯЕЭГЕФПеМфЛЎЗжЮЊЖрИіЯИАћЃЈВЛвЊгыЩњЮяЯИАћЛьЯ§ЃЉЃЌВЂМЦЫуУПИіЯИАћФкЕФЖЬЪБЕЏЕРЃЈshort-time trajectoriesЃЉЃЌвдЙЙНЈУшЪіЯИАћжЎМфЙ§ЖЩЕФЖЏСІбЇЗНАИЁЃЫќЪЕЯжСЫвЛЪЏЖўФёЃЈIt kills two birds with one stoneЃЉЃЌвђЮЊЫќПЩвдздЖЏЬсЙЉЯЕЭГЕФЭГМЦУшЪіЃЌВЂЧвБШТљСІдЫЫуИќгааЇЁЃ
ЫцЛњЕФЁЂжїЗНГЬЪНЕФЩњЮяЯИАћФЃФтЗНЗЈПЩвдПДзїЪЧЯИАћЕФвЛжжМЋЯоЧщПіЃЌЖјетжжЧщПігыдзгНтЮіЙьМЃЕФЙиЯЕВЂВЛУїЯдЁЃNetz КЭ Eaton ЕФЙРМЦБэУїЃЌМДЪЙЪЙгУЯжДњМЦЫузЪдДЃЌЖдЩњЮяЯИАћЃЈЖјЗЧДѓФдЃЁЃЉЕФетжжФЃФтвВЪЧПЩвдДяЕНЕФЁЃ
ШЛЖјЃЌГ§СЫЫцЛњжїЗНГЬЗЈЕФНќЫЦаджЪЭтЃЌЫќЛЙУцСйзХЫЋжиЬєеНЁЃЪзЯШЃЌИУЗНЗЈашвЊЪТЯШСЫНтЫљгаЯрЙиЕФЛЏбЇЗНГЬЪНЯИАћФкЕФаЮГЩЁЃетгавЛИіжиДѓЕФОжЯоЃЌвђЮЊбаОПепЯЃЭћЭЈЙ§ФЃФтЗЂЯжДЫЧАЮДБиФмдЄСЯЕНЕФаТЛЏбЇЙ§ГЬЁЃЙцБмДЫЯожЦЕФвЛжжЧБдкЗНЗЈЪЧдкЖЏЬЌЕиЗЂЯжПЩФмЕФЖЏСІбЇЪТМўЃЈЛЏбЇзЊЛЏЃЉЕФЧщПіЯТЃЌВЩгУздЪЪгІЗНЗЈЁЃ
ЦфДЮЃЌИУЗНЗЈвЊЧѓНЋУПжжПЩФмЕФЛЏбЇзЊЛЏЕФЫйТЪЯЕЪ§зїЮЊЪфШыЁЃГ§ЗЧЪЕбщПЩгУЃЌЗёдђДЫРраХЯЂБиаыРДзддзгФЃФтЁЊЁЊавдЫЕФЪЧЃЌжДааВйзїЕФЙцФЃвЊБШећИіЩњЮяЯИАћЕФЙцФЃаЁЕУЖрЁЃЭЌбљЃЌдкетРяЃЌбаОПШЫдБашвЊПМТЧЕМжТЫйТЪЙРМЦЕФМЦЫуЕФзМШЗадЁЃЩЯУцвбОЬжТлСЫвЛжжЮѓВюРДдДЃЌМДЗжзгФмСПЙРМЦЕФзМШЗадЃЌЕЋЪЧгЩгкВЮЪ§ЪфШыЕНЗНГЬжаЃЌЫљвдРЇФбВЂУЛгаОЭДЫНсЪјЁЃИУФЃФтШдШЛашвЊМЦЫуЁЃетбљзіЕФвЛжжжБНгЗНЗЈЪЧдкЗДгІЮязДЬЌЯТЦєЖЏИааЫШЄЕФЗжзгЯЕЭГЃЌЕШЕНЗДгІЭъГЩЃЈМДДяЕНЗДгІВњЮяЃЉЃЌШЛКѓжиИДФЃФтЃЌжБЕНЙРМЦГіЦНОљЗДгІЪБМфЮЊжЙ[9]ЁЃ
3. аТЕФЕЭГЩБОФЃФтЗНЗЈ
вЛжжИќЕЭГЩБОЕФЬцДњЗНЗЈЪЧЙ§ЖЩЬЌРэТлЃЌетЪЧУПБОЛЏбЇНЬПЦЪщжаЖМНВЕФНќЫЦЗНЗЈЁЃВЛавЕФЪЧЃЌЯждкЮвУЧжЊЕРЙ§ЖЩЬЌРэТлЖдвКЯрЛЏбЇЖЏСІбЇЕФУшЪіаЇЙћВЛОЁШЫвтЁЃвђДЫЃЌШЫУЧНЋВЛЕУВЛЫпжюИќзМШЗЕФЁЂЯргІвВИќАКЙѓЕФЗНЗЈЁЃзд1970ФъДњЦ№ЃЌЛЏбЇЮяРэбЇНчПЊЗЂСЫаэЖрЗНЗЈРДМЦЫуЁАОЋШЗЕФЁБЗДгІЫйТЪЃЌЖјЮоашНјааГЄЪБМфЕФЖЏСІбЇФЃФт[7]ЃЌЭЈГЃЕФЯыЗЈЪЧдкЗДгІЮяКЭВњЮязДЬЌжЎМфНјааФЃФтЃЌВЂЖдЯЕЭГНјааМрПиЁЃжБЕНЕНДяВњЦЗЮЊжЙЁЃетбљЃЌПЩвдЪЙгУЯрЖдНЯЖЬЕФЙьМЃ[7]РДМЦЫуЖдЙ§ЖЩЬЌРэТлЕФЖЏЬЌаЃе§ЁЃ

ЭМ4. 2016ФъХЕБДЖћЛЏбЇНБНБРјСЫЗжзгЛњЦїЕФЯрЙиЙЄзїЃЌЖдЩњЮяЗжзгЛњЦїЕФбаОПНЋДйНјЮЂЙлГпЖШМЦЫуЛњФЃФтЕФЪЕЯж
ЖдЕЅИіЯИАћКЭЖрЯИАћЯЕЭГНјааФЃФтЕФСэвЛИіеЯАЪЧЃЌетжжФЃФтВЛЪЧЖРСЂЕФЃЌБиаывРРЕгкгаЙиЯИАћЗжзгзщжЏЕФНсЙЙаХЯЂЁЃЬиБ№ЪЧОЭЗжзгЛњЦїЕФФкВПдЫааЖјбдЃЌИУаХЯЂБиаыРДздЪЕбщбаОПЃЌФПЧАЩаВЛЭъећЁЃ
змНсЩЯЪіЙлЕуЃЌОЁЙмПЩФмдкЮДРДМИЪЎФъФкЪЕЯжећИіЯИАћЕФМЦЫуЛњФЃФтЃЌЕЋШЫУЧВЛгІИУНЋЫљгаЕФГяТыЖМбКзЂгкЫќУЧзїЮЊбЇЯАЩњУќЮяжЪЕФжївЊЙЄОпЕФаЇгУЁЃЕквЛаддРэФЃФтЖрЯИАћзАХфЬхЃЈШчДѓФдЃЉЕФЧАОАИќМгїіЕЁЃСэвЛЗНУцЃЌЫљгаетаЉПМТЧЖМЪЧЛљгкЖдЯжгаЗТецЙЄОпЕФЭЦТлЃЌШЫУЧгРдЖЖМВЛгІЕЭЙРПЦбаШЫдБЕФДДдьСІЁЃЕБЧАдкМЦЫуПЦбЇЁЂМЦЫуЛњгВМўКЭЩњУќПЦбЇЗНУцЮоЗЈдЄСЯЕФЭЛЦЦПЩФмЛсЪЙЮвУЧГЏзХФПБъТѕНјМЦЫуЛњФЃФтЩњЮябЇЕФЫйЖШИќПьЁЃ
ВЮПМЮФЯз
1. E. Schrödinger, What is Life? The Physical Aspect of the Living Cell (Cambridge University Press, 1944).
2. R. R. Netz, W. A. Eaton, Estimating computational limits on theoretical descriptions of biological cells. Proc. Natl. Acad. Sci. U.S.A., 10.1073/pnas.2022753118 (2021).
3. K. Lindorff-Larsen, S. Piana, R. O. Dror, D. E. Shaw, How fast-folding proteins fold. Science 334, 517ЈC520 (2011).
4. I. Yu et al., Biomolecular interactions modulate macromolecular structure and dynamics in atomistic model of a bacterial cytoplasm. eLife 5, e19274 (2016).
5. G. Henkelman, H. Jo ́ nsson, T. Lelièvre, N. Mousseau, A. F. Voter, ЁАLong-timescale simulations: Challenges, pitfalls, best practices, for development and applicationsЁБ in Handbook of Materials Modeling, W. Andreoni, S. Yip, Eds. (Springer, 2020), pp. 1ЈC10.
6. M. Bogojeski, L. Vogt-Maranto, M. E. Tuckerman, K. R. Müller, K. Burke, Quantum chemical accuracy from density functional approximations via machine learning. Nat. Commun. 11, 5223 (2020).
7. R. Elber, D. E. Makarov, H. Orland, Molecular Kinetics in Condense Phases: Theory, Simulation, and Analysis (John Wiley, 2020).
8. R. Elber, Perspective: Computer simulations of long time dynamics. J. Chem. Phys. 144, 060901 (2016).
9. G. Henkelman, H. Jo ́ nsson, Long time scale kinetic Monte Carlo simulations without lattice approximation and predefined event table. J. Chem. Phys. 115, 9657ЈC9666 (2001).
РДдДЃКжаПЦдКИпФмЫљ
|
|
|